How is the KL loss computed?
See original GitHub issueThanks for the great work!
There’s one thing that confuses me very much though. In the paper, the KL loss is computed as (Eq.3) .
In vanilla VAEs, the KL loss is actually an expectation. As the two distributions involved are both Gaussians, there is a closed-form expression. It is understandable that as the distribution
is no more a Gaussian in VITS, we don’t calculate the expectation but instead use the sampled
to evaluate the probability density of
and calculate Eq.3. Till now, there is no problem for me.
Nevertheless, in the code I notice that the KL loss is calculated in a special way, in losses.py:kl_loss(z_p, logs_q, m_p, logs_p, z_mask). In this function, as far as I know, m_p and logs_p are extracted from text encodings, and logs_q is extracted from spectrogram posterior encoder. z_p is the flow-transformed latent variable from posterior encoder. And this function calculates KL loss as the sum of and
. So how does this come? I guess the first term comes from Eq.4 but why is the log-determinant missing? Also, why is
not participating in this loss? I really cannot relate this calculation with Eq.3 in the paper.
There is another question by the way. I notice that the mean_only switch is turned off in the ResidualCouplingLayer, which means the log-determinant returned by the flow is always 0. In this case, the transformed distribution is still a Gaussian, right?
Again, thanks for the work and code!
Issue Analytics
- State:
- Created 2 years ago
- Reactions:5
- Comments:5

 Top Related StackOverflow Question
Top Related StackOverflow Question
@cantabile-kwok I think I figured it out. First, about the log-determinant, in the section 2.5.2 of the paper it is said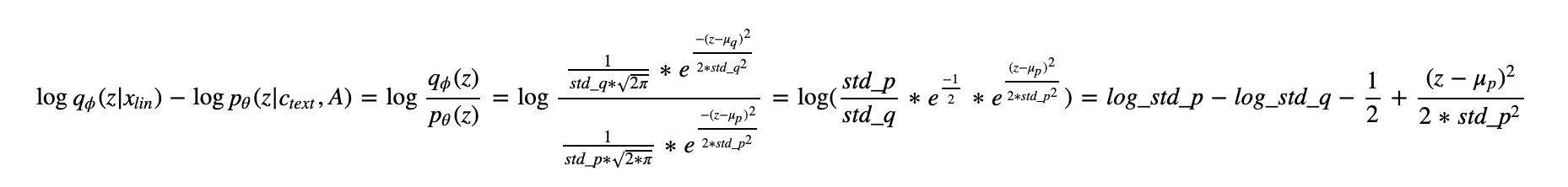 The second equation is true since both q and p are normal distributions, next equation is true since z is computed as
The second equation is true since both q and p are normal distributions, next equation is true since z is computed as
we design the normalizing flow to be a volume-preserving transformation with the Jacobian determinant of one, by the definition,volume-preserving transformationis a transformation with log-determinant equals to zero, andnot volume-preserving transformationis a transformation with non-zero log-determinant. In the code it can be seem here, as you rightly said, it’s because ofmean_onlyflag. Second, about the loss, let’s take a look at Eq. 3.z = \mu_q + eps * \std_qso the exponent in the numerator becomee^(-1/2)and when we get log from the whole expression we get exactly thekl_loss, hope it was useful and clear, feel free to ask any questions.@AndreyBocharnikov Yes, I agree with u