TypeScripts Type System is Turing Complete

This is not really a bug report and I certainly don’t want TypeScripts type system being restricted due to this issue. However, I noticed that the type system in its current form (version 2.2) is turing complete.

Turing completeness is being achieved by combining mapped types, recursive type definitions, accessing member types through index types and the fact that one can create types of arbitrary size. In particular, the following device enables turing completeness:

type MyFunc<TArg> = {
  "true": TrueExpr<MyFunction, TArg>,
  "false": FalseExpr<MyFunc, TArg>
}[Test<MyFunc, TArg>];

with TrueExpr, FalseExpr and Test being suitable types.

Even though I didn’t formally prove (edit: in the meantime, I did - see below) that the mentioned device makes TypeScript turing complete, it should be obvious by looking at the following code example that tests whether a given type represents a prime number:

type StringBool = "true"|"false";

interface AnyNumber { prev?: any, isZero: StringBool };
interface PositiveNumber { prev: any, isZero: "false" };

type IsZero<TNumber extends AnyNumber> = TNumber["isZero"];
type Next<TNumber extends AnyNumber> = { prev: TNumber, isZero: "false" };
type Prev<TNumber extends PositiveNumber> = TNumber["prev"];


type Add<T1 extends AnyNumber, T2> = { "true": T2, "false": Next<Add<Prev<T1>, T2>> }[IsZero<T1>];

// Computes T1 * T2
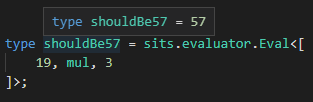
type Mult<T1 extends AnyNumber, T2 extends AnyNumber> = MultAcc<T1, T2, _0>;
type MultAcc<T1 extends AnyNumber, T2, TAcc extends AnyNumber> = 
		{ "true": TAcc, "false": MultAcc<Prev<T1>, T2, Add<TAcc, T2>> }[IsZero<T1>];

// Computes max(T1 - T2, 0).
type Subt<T1 extends AnyNumber, T2 extends AnyNumber> = 
		{ "true": T1, "false": Subt<Prev<T1>, Prev<T2>> }[IsZero<T2>];

interface SubtResult<TIsOverflow extends StringBool, TResult extends AnyNumber> { 
	isOverflowing: TIsOverflow;
	result: TResult;
}

// Returns a SubtResult that has the result of max(T1 - T2, 0) and indicates whether there was an overflow (T2 > T1).
type SafeSubt<T1 extends AnyNumber, T2 extends AnyNumber> = 
		{
			"true": SubtResult<"false", T1>, 
            "false": {
                "true": SubtResult<"true", T1>,
                "false": SafeSubt<Prev<T1>, Prev<T2>>
            }[IsZero<T1>] 
		}[IsZero<T2>];

type _0 = { isZero: "true" };
type _1 = Next<_0>;
type _2 = Next<_1>;
type _3 = Next<_2>;
type _4 = Next<_3>;
type _5 = Next<_4>;
type _6 = Next<_5>;
type _7 = Next<_6>;
type _8 = Next<_7>;
type _9 = Next<_8>;

type Digits = { 0: _0, 1: _1, 2: _2, 3: _3, 4: _4, 5: _5, 6: _6, 7: _7, 8: _8, 9: _9 };
type Digit = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9;
type NumberToType<TNumber extends Digit> = Digits[TNumber]; // I don't know why typescript complains here.

type _10 = Next<_9>;
type _100 = Mult<_10, _10>;

type Dec2<T2 extends Digit, T1 extends Digit>
	= Add<Mult<_10, NumberToType<T2>>, NumberToType<T1>>;

function forceEquality<T1, T2 extends T1>() {}
function forceTrue<T extends "true">() { }

//forceTrue<Equals<  Dec2<0,3>,  Subt<Mult<Dec2<2,0>, _3>, Dec2<5,7>>   >>();
//forceTrue<Equals<  Dec2<0,2>,  Subt<Mult<Dec2<2,0>, _3>, Dec2<5,7>>   >>();

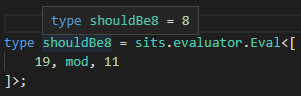
type Mod<TNumber extends AnyNumber, TModNumber extends AnyNumber> =
    {
        "true": _0,
        "false": Mod2<TNumber, TModNumber, SafeSubt<TNumber, TModNumber>>
    }[IsZero<TNumber>];
type Mod2<TNumber extends AnyNumber, TModNumber extends AnyNumber, TSubtResult extends SubtResult<any, any>> =
    {
        "true": TNumber,
        "false": Mod<TSubtResult["result"], TModNumber>
    }[TSubtResult["isOverflowing"]];
    
type Equals<TNumber1 extends AnyNumber, TNumber2 extends AnyNumber>
    = Equals2<TNumber1, TNumber2, SafeSubt<TNumber1, TNumber2>>;
type Equals2<TNumber1 extends AnyNumber, TNumber2 extends AnyNumber, TSubtResult extends SubtResult<any, any>> =
    {
        "true": "false",
        "false": IsZero<TSubtResult["result"]>
    }[TSubtResult["isOverflowing"]];

type IsPrime<TNumber extends PositiveNumber> = IsPrimeAcc<TNumber, _2, Prev<Prev<TNumber>>>;
    
type IsPrimeAcc<TNumber, TCurrentDivisor, TCounter extends AnyNumber> = 
    {
        "false": {
            "true": "false",
            "false": IsPrimeAcc<TNumber, Next<TCurrentDivisor>, Prev<TCounter>>
        }[IsZero<Mod<TNumber, TCurrentDivisor>>],
        "true": "true"
    }[IsZero<TCounter>];

forceTrue< IsPrime<Dec2<1,0>> >();
forceTrue< IsPrime<Dec2<1,1>> >();
forceTrue< IsPrime<Dec2<1,2>> >();
forceTrue< IsPrime<Dec2<1,3>> >();
forceTrue< IsPrime<Dec2<1,4>>>();
forceTrue< IsPrime<Dec2<1,5>> >();
forceTrue< IsPrime<Dec2<1,6>> >();
forceTrue< IsPrime<Dec2<1,7>> >();

Besides (and a necessary consequence of being turing complete), it is possible to create an endless recursion:

type Foo<T extends "true", B> = { "true": Foo<T, Foo<T, B>> }[T];
let f: Foo<"true", {}> = null!;

Turing completeness could be disabled, if it is checked that a type cannot use itself in its definition (or in a definition of an referenced type) in any way, not just directly as it is tested currently. This would make recursion impossible.

//edit: A proof of its turing completeness can be found here

[fc01]

• 👾 Sokoban Game in Pure TypeScript Type System

• Repo: https://github.com/fc01/TypeGame

• 

[fightingcat]

@RyanCavanaugh I’m almost done, have implemented parser and arithmetics, right now there is a working expression evaluator, I’ve pushed to the repo.