Numpy eigh crashes - unexpected results

I have an adjacency matrix of a graph and then I build the Laplacian matrix of the graph (https://en.wikipedia.org/wiki/Laplacian_matrix) as L = D - A, where D is the degree matrix and A is the adjacency matrix of the graph.

Data: https://file.io/StnNei0y7vxP

Code:

from scipy.io import loadmat
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

X = np.array(loadmat('/Users/sera/Downloads/113922_TCS_Glasser360.mat')['TCS'])

# build adjacency
X = stats.zscore(X, axis=1)
u, l = 0.0, 0.0
Xu, Xl = np.zeros((X.shape), dtype=np.float64), np.zeros((X.shape), dtype=np.float64)
Xu[X >= u] = X[X >= u] 
Xl[X <= l] = X[X <= l] 
Ac = (np.dot(Xu, Xu.T) + np.dot(Xl, Xl.T) ) / (Xu.shape[1]-1.)
np.fill_diagonal(Ac,0.0)

# plot the adjacency
plt.imshow(Ac);plt.colorbar()
plt.show()

# build laplacian
D = np.diag(np.sum(Ac,axis=1))
L = D - Ac

# eigh
l, v = np.linalg.eigh(L)
i = l.argsort() # sorting
l, v = l[i], v[:,i]

# scree plot of eigenvalues
plt.plot(l[:], 'o-')
plt.show()

# plot first eigenvector -should be constant
plt.plot(v[:,0])
plt.show()

# Sanity check 1: plot fiedler vector -- should be smooth
plt.plot(v[:,1])
plt.show()

# Sanity check 2: it must be $ L  v[:,i] -\lambda v[:,i] = 0 $ for every $i$
ii=1;
plt.plot(np.dot(L, v[:,ii]) - l[ii]*v[:,ii])
plt.show()

The plt.plot(v[:,1]) returns:

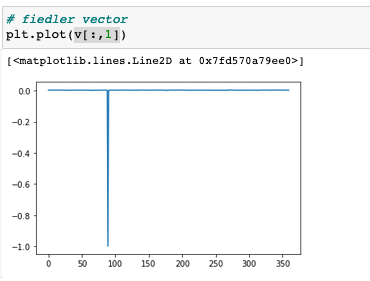
and it is obvious that the spike and this eigenvector is a product of a crashed algorithm.

Why does this happen? How can I solve this?

[melissawm]

By spikes, I assume you mean the variation in the values in the graph. However, the scale of the graph is very small - around 1e-13. So that effectively means that np.dot(L, v[:,ii]) - l[ii]*v[:,ii] is 0 (up to floating point precision). In addition, since v[:, 1] must be a non-zero vector, it makes sense that one of its entries has value -1. Also, np.dot(v.T, v) is effectively the identity matrix which further confirms that this computation is reasonable.

[rkern]

Also, we see that the Ac.mean(axis=0).argmin() is 89, the same as v[:, 1].argmin(). That node is indeed uniquely picked out by the adjacency data, so it should not be surprising that it is the lone negative in the Fiedler vector.

Given that the eigenvalues and eigenvectors seem to obey the expected properties up to numerical precision, I don’t see any evidence of a problem here.