Create functions for computing various prediction horizons.

Currently, xr_predictability_horizon is a simple test for finding the lead time to which the initialized skill beats out persistence/uninitialized.

def xr_predictability_horizon(skill, threshold, limit='upper'):
    """
    Get predictability horizons of dataset from skill and
    threshold dataset.
    """
    if limit is 'upper':
        ph = (skill > threshold).argmin('time')
        # where ph not reached, set max time
        ph_not_reached = (skill > threshold).all('time')
    elif limit is 'lower':
        ph = (skill < threshold).argmin('time')
        # where ph not reached, set max time
        ph_not_reached = (skill < threshold).all('time')
    ph = ph.where(~ph_not_reached, other=skill['time'].max())
    return ph

However, it does not account for two forms of statistical significance: (1) Need to check first that the skill of the initialized prediction (pearson correlation coefficient) is significant (p < 0.05 for example). (2) Need to then check the point to which the initialized skill is significantly different from the uninitialized skill. You first do a Fisher r to z transformation so that you can compare the correlations one-to-one. Then you do a z-score comparison with a lookup table to seek significance to some confidence interval.

Fisher’s r to z transformation:

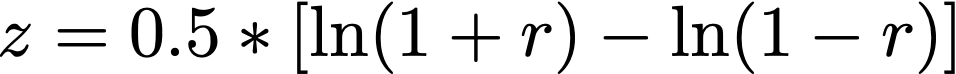
z-comparison: https://www.statisticssolutions.com/comparing-correlation-coefficients/

z-score thresholds for different confidence levels:

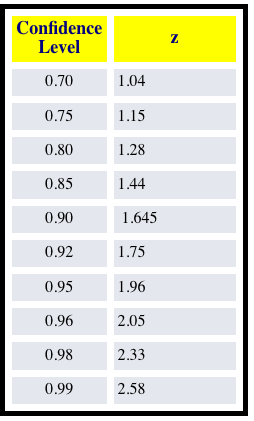
I’ve written up this code in my personal project, so I just need to transfer it over to the package:

def z_significance(r1, r2, N, ci='90'):
    """Returns statistical significance between two skill/predictability
    time series.
    Example:
        i_skill = compute_reference(DPLE_dt, FOSI_dt)
        p_skill = compute_persistence(FOSI_dt, 10)
        # N is length of original time series being
        # correlated
        sig = z_significance(i_skill, p_skill, 61)
    """
    def _r_to_z(r):
        return 0.5 * (log(1 + r) - log(1 - r))

    z1, z2 = _r_to_z(r1), _r_to_z(r2)
    difference = np.abs(z1 - z2)
    zo = difference / (2 * sqrt(1 / (N - 3)))
    # Could broadcast better than this, but this works for now.
    confidence = {'80': [1.282]*len(z1),
                  '90': [1.645]*len(z1),
                  '95': [1.96]*len(z1),
                  '99': [2.576]*len(z1)}
    sig = xr.DataArray(zo > confidence[ci], dims='lead time')
    return sig

[aaronspring]

I think this should be a very generic function. get some criterion as input and then just do some kind .argmin('lead') and properly masking nans.

[aaronspring]

Reimplementation suggestion:

• get a pvalue from z score or bootstrapping
• get PH as last lead where p smaller than psig = 0.05 default
• Test on 1d and 3d fields based on sample output