Qiskit function to encode Python list of integers into quantum state

Suppose I am given the following Python list/array as an example:

arr = [2, 1, 2, 0, 0, 1, 3, 2]

To encode this data into a quantum state I can use the “bit-string basis encoding” technique, writing both the integer elements and the integer indices of arr as binary strings $s \in \{ 0,1 \}^*$ and then transforming them into a quantum state on the computational basis. In this case, I would need $n=3$ qubits to encode the indices $i=0,\dots,N-1$ with $N=2^n=8$ and $n_*=2$ more qubits to encode the digits $\mathrm{arr}_i\in \{ 0,1,2,3 \}$, ending up with the following state:

$$|\psi \rangle = \frac{1}{\sqrt{N}} \sum_{i=0}^{N-1} |\mathrm{arr}_i \rangle |i\rangle$$

The Qiskit code implementing the quantum circuit to prepare the state $|\psi \rangle$ would look like this:

from qiskit import QuantumRegister, QuantumCircuit
from qiskit.circuit.library.standard_gates import C3XGate

qr1 = QuantumRegister(size=3, name='index')
qr2 = QuantumRegister(size=2, name='element')

encoder = QuantumCircuit(qr1, qr2)
encoder.h(qr1)
encoder.append(C3XGate(ctrl_state='000'), [*qr1, qr2[1]])
encoder.append(C3XGate(ctrl_state='001'), [*qr1, qr2[0]])
encoder.append(C3XGate(ctrl_state='010'), [*qr1, qr2[1]])
encoder.append(C3XGate(ctrl_state='101'), [*qr1, qr2[0]])
encoder.append(C3XGate(ctrl_state='110'), [*qr1, qr2[0]])
encoder.append(C3XGate(ctrl_state='110'), [*qr1, qr2[1]])
encoder.append(C3XGate(ctrl_state='111'), [*qr1, qr2[1]])

encoder.draw('mpl')

Questions:

1. Is this correct? Are there more efficient techniques for data encoding?
2. Does Qiskit provide any functionality to automatically prepare the quantum state given a generic Python list?

[SimoneGasperini]

Ok thank you @ShellyGarion! So there we are actually implementing “amplitude encoding”, right? I run that circuit by using the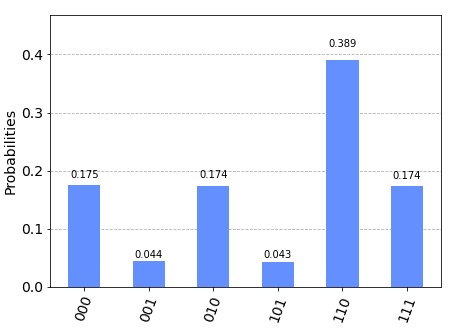 qasm_simulator backend and the final measurements on the 3-qubits-system are the following:

Makes sense! The probabilities seems indeed to correspond to the square of each entry in the original (normalized) array:

(arr / norm)**2 = [0.174, 0.043, 0.174, 0.0, 0.0, 0.043, 0.391, 0.174]

[Cryoris]

1. I’m not an expert on which would be the most efficient way of synthesizing this network (@ShellyGarion or @alexanderivrii would certainly know more!) but conceptually this looks correct to me. In general there are different techniques to encode numbers into quantum states, here you mention basis encoding but there’s also amplitude encoding, phase encoding, angle encoding… depending on your use case either might be better! This would only change what you control though, not the logic on the index register.
2. There’s currently no functionality to encode a list of numbers, no. But if there’s a common use-case where this is required we can certainly discuss adding it 🙂