Numerical instabilities with occultations of very high order maps

Hi Rodrigo, I noticed that flux sometimes diverges for occultations in both emitted and reflected light with very high order maps (l > 20). Here’s a reproducible example:

map = starry.Map(ydeg=25, reflected=False)
map.add_spot(amp=0.01, sigma=0.01, lat=41., lon=20.)

xo = np.linspace(-1, 1, 100)
yo = np.linspace(-0.08, -0.132, 100)
zo = np.ones(len(xo))
ro = 0.8552
theta = np.linspace(28.5, 28.7, 100)

flux = map.flux(theta=theta, xo=xo, yo=yo, zo=zo, ro=ro)

fig, ax = plt.subplots(2, 1, figsize=(5, 5))

ax[0].set_xlim(-1.1, 1.1)
ax[0].set_ylim(-1.1, 1.1)
ax[0].axis("off")
ax[0].imshow(map.render(), origin="lower", cmap="plasma", extent=(-1, 1, -1, 1))
npts = len(xo)
for n in list(range(0, npts, npts // 3)) + [npts - 1]:
    circ = plt.Circle(
        (xo[n], yo[n]), radius=ro, color="k", fill=True, clip_on=False, alpha=0.2
    )
    ax[0].add_patch(circ)
    
ax[1].plot(flux, 'k.')

And this is the output:

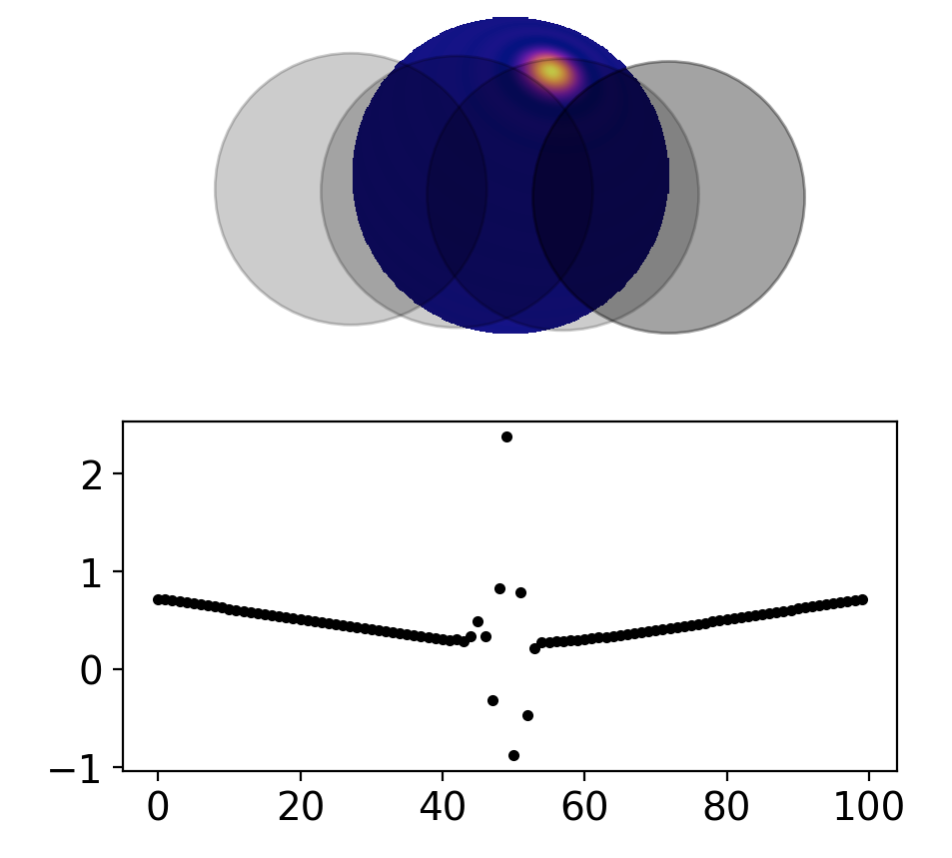
It’s an edge case that probably doesn’t matter for inference. I noticed it because I generate fake data from very high order maps.

Starry version:'1.0.1.dev43+gf871d249'

[rodluger]

Ok, thanks for finding this. Here’s a slightly simpler version that shows the instability as a function of k^2 (Equation D23 in the paper):

import starry
import matplotlib.pyplot as plt
import numpy as np
starry.config.lazy = False

map = starry.Map(ydeg=20, reflected=False)
map[1:, :] = 1
xo = np.logspace(-2, np.log10(2.0), 10000)
yo = 0
ro = 0.9
flux = map.flux(xo=xo, yo=yo, ro=ro)
bo = np.sqrt(xo ** 2 + yo ** 2)
ksq = (1 - ro ** 2 - bo ** 2 + 2 * bo * ro) / (4 * bo * ro)
plt.plot(ksq, flux)
plt.xscale("log")
plt.show()

Looks like things are bad for k^2 > 1, although the instability sets in a bit before that. My guess is the evaluation of the J integral (Equation D39) gets unstable. It might help to replace the upward/downward recursion with a tridiagonal solver. I’ll look into it.

[rodluger]

Punting on this for now. Feel free to reopen if a better solution is needed.