MyGrad 0.6: Refactoring back-propagation system

I’d like to discuss the back-prop refactor that MyGrad will undergo. I hope to arrive at a clean, simple, and efficient implementation design before beginning to restructure the code. I’ve already implemented a hacky branch with the relevant fundamental changes, and it works as a proof-of-concept.

The following reflects my current thoughts on the refactor and some barriers that I am anticipating. I’d love to get other perspectives on approaches for implementing breadth-first back-prop.

Motivation

MyGrad’s current back-propagation system, although elegant in its simplicity, fails catastrophically - in terms of computational efficiency - for branching graphs such as:

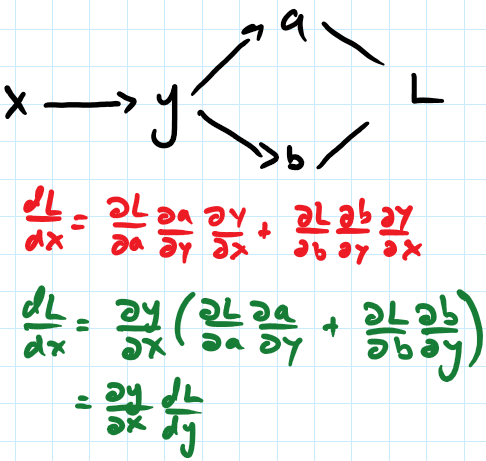
Currently, we back-propagate depth-first. This means that y simply back-props each of its incoming gradients to x. As a result, dy/dx is computed twice. This current procedure is represented by the red equation.

A breadth-first approach, conveyed by the green equation, would entail first accumulating all of y’s partial derivatives, constructing the total derivative of the terminal node (L) w.r.t y, and back-propagating to x a single time.

While the breadth-first approach is at most twice as fast for this simple example, back-propagation through a computational graph for a simple gated RNN is intractable without this method.

Originally, we had written MyGrad’s back-prop system in such a way that students could easily trace through it or even implement it on their own. Moving forward, students can still be asked to construct their own back-prop systems in this way. An additional lesson will need to be provided to present the additional scaffolding needed to support breadth-first back-propagation.

Implementation Considerations

A breadth-first back-propagation system, by which a variables only back-propagated total derivatives, is substantially more cumbersome than is the current depth-first approach.

Each variable in the graph must know about all of its down-stream usages in the computational graph, distinguishing between those operations that do and do not contribute to the terminal node, which invoked the back-propagation; this is required in order for a variable to know when it has finished constructing the total derivative.

The following graph reveals a couple of the complexities that arise when accounting for these things:

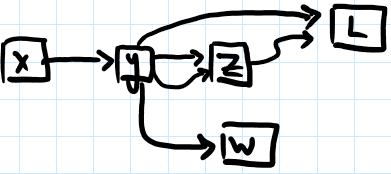
Here, invoking back-prop from L requires y to accumulate its derivatives from:

• its direct contribution to L
• both of its contributions to z (e.g. z = y * y)

and then propagate this derivative to x. See that y should not wait for a derivative from w, as w is spurious to the value of L.

Implementation Ideas

• backward needs to be refactored such that there is a public method, which distinguishes the terminal node for the computational graph. This will invoke _backward on all subsequent tensors, which will impose the constraint that a tensor will not back-prop until its received derivatives from all relevant down-stream operations. It would also be used to signal that a “new” back-propagation has begun; this is necessary in order for people to be able to do:

  loss.backward()
  loss.null_gradients()
  loss.backward()
  

  and get the same results. That is, invoking public backward should cause each variable to again expect all relevant downstream derivatives before itself back-propping.
• Although a tensor already holds a list, _ops of the operation-instances that it is involved in, it may be preferable to work with hashable IDs for these operations, so that we can leverage set-comparisons for distinguishing spurious branches in the graph. That being said, we must also accommodate graphs like those above where a single tensor serves as multiple inputs to a single operation. Using a set would remove this information. I’m not sure what the right approach is for this.
• Currently, null_gradients also clears the computational graph by clearing each tensor’s _ops list. Now that we have to explicitly leverage this information, calling null_gradients prior to back-prop would be problematic. We may need to have a separate clear_graph function instead, so that people can use the popular workflow:

  loss.null_gradients()
  loss.backward()
  optim.step()
  

[davidmascharka]

Disclaimer: I haven’t really dived into the implementation details of what Ryan did and haven’t looked through MyGrad in a lot of depth.

My initial thought would be to topologically sort the computational graph. We know this is possible because everything we create is going to be a DAG; if can’t possibly have cycles or we’d never finish computation. This ensures there is a topological sorting possible.

A depth-first traversal will run in linear time since you just have to visit each node in the graph once. Once you’ve got the topological sort, you can iterate through it from the end point in the graph and send the gradient back. Pop that out of the queue and move on to backwarding the next op’s grad.

This does add some complexity to the implementation, but it should be relatively straightforward still as a teaching tool, I’d imagine.

[rsokl]

Good point