`_cdf_cvm` inaccurate for small `n`

The documentation of _cdf_cvm notes:

The function is not expected to be accurate for large values of x, say x > 2, when the cdf is very close to 1 and it might return values > 1 in that case, e.g. _cdf_cvm(2.0, 12) = 1.0000027556716846.

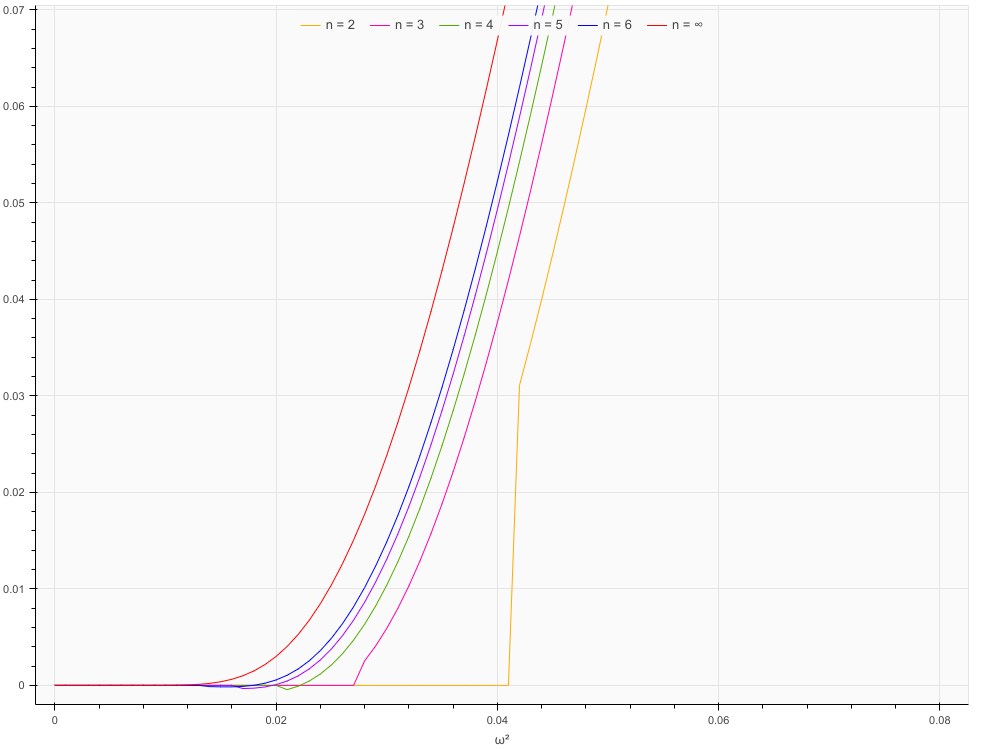
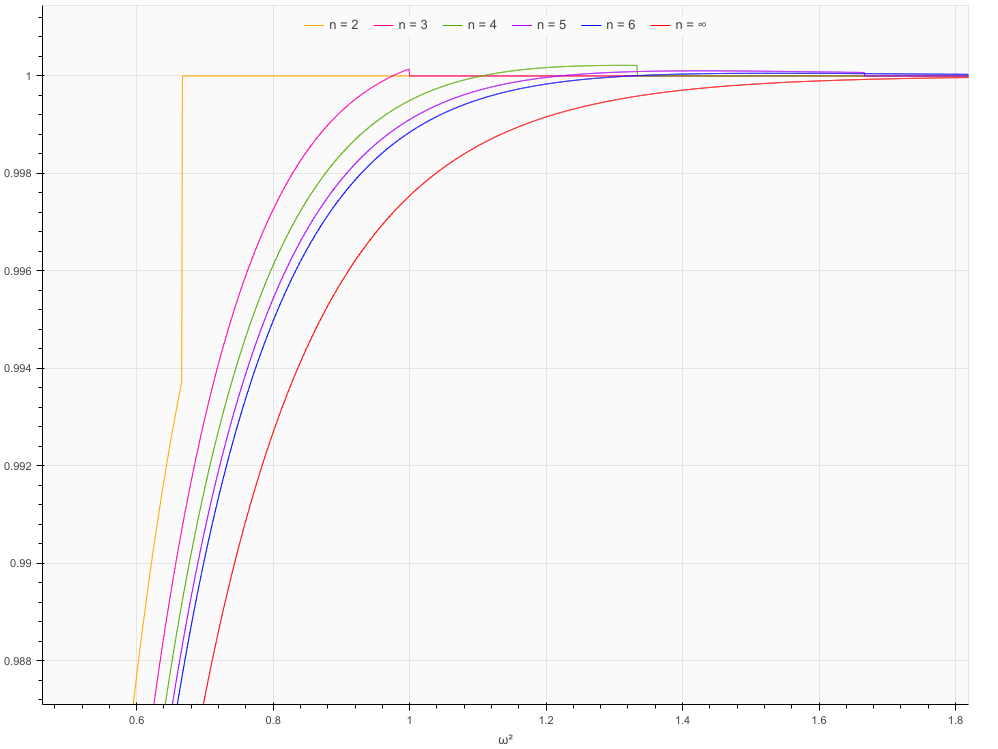
However, in addition to that, the function is inaccurate for small values of n, in particular 2. Below approx. 0.042 the value drops to 0, and above approx. 0.666 it jumps to 1. To a smaller extent, similar things happen for other small n.

I don’t know whether this can be fixed, but it should be documented.

Reproducing code example:

>>> _cdf_cvm([0.041, 0.042, 0.666, 0.667], n=2)
array([0.      , 0.031081, 0.993724, 1.      ])

Scipy/Numpy/Python version information:

1.6.3 1.20.2 sys.version_info(major=3, minor=8, micro=8, releaselevel='final', serial=0)

Plots

[chrisb83]

Hi,

if you check the second reference in the documenation, you will find some more details on the approximation:

Csorgo, S. and Faraway, J. (1996). The Exact and Asymptotic Distribution of Cramér-von Mises Statistics. Journal of the Royal Statistical Society, pp. 221-234. => you can find it on the website https://people.bath.ac.uk/jjf23/papers/index.html

Below approx. 0.042 the value drops to 0, and above approx. 0.666 it jumps to 1

That is correct, the support of the exact distribution is contained in [1/(12*n), n/3], see Eq 1.1 in the article

You can take a look at Table 1 in the article, it contains a comparison of the exact values and the approximation. And indeed, for n=2, the approximation is not great but that is not a problem with the implementation but rather the way the approximation works (error is about 1/n**2, see Eq 1.8)

So if you need more accurate values for small n, there are other approaches you could use, they are briefly mentioned in the article, too. I hope it helps…

[allefeld]

I’ve created a PR, please check.

@chrisb83:

I don’t understand the problems of the approximation well enough to say whether it would be feasible to make a more precise implementation. I suspect that would entail numerical calculations that are too expensive for the function itself, so one would probably have to pre-calculate a tabulation and then interpolate.

I agree that there is no acute problem for the GoF test, because it is unlikely that anyone would do such a test on a sample of 2 or similar, and even then at the conventional level of 0.05 one would have to Bonferroni-correct for several tests in order to reach the values where the approximation fails relevantly.

I would still appreciate if the function (either the current approximation or something better) could be exposed publicly. scipy.special seems like a good place for that.