BUG: scipy.stats.theilslopes intercept calculation can produce incorrect results.

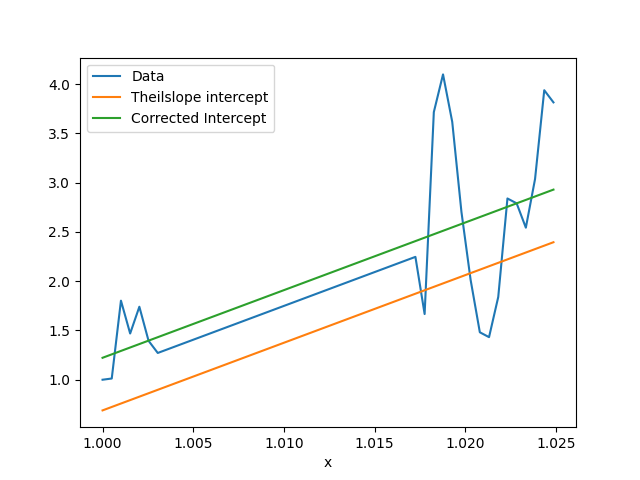
Theilslopes calculates the median intercept using the calculated theilslope estimate and the median x and median y values as: np.median(y) - medslope * np.median(x). This can produce an incorrect intercept when there is a gap in the middle of the x values. Most other implementations of this algorithm use the median of all intercepts np.median(y - medslope * x), which doesn’t seem to have this issue.

The np.median(y) - medslope * np.median(x) is in the documentation, so I’m not entirely sure if there’s a good reason for doing calculating the intercept that way.

Reproducing code example:

import pandas as pd
from scipy.stats import theilslopes
from io import StringIO
import matplotlib.pyplot as plt

test_data = StringIO("""
x,y
1,1
1.000507357,1.012345679
1.001014713,1.802469136
1.00152207,1.469135802
1.002029427,1.740740741
1.002536783,1.395061728
1.00304414,1.271604938
1.017250127,2.24691358
1.017757484,1.666666667
1.01826484,3.716049383
1.018772197,4.098765432
1.019279554,3.617283951
1.01978691,2.703703704
1.020294267,2.012345679
1.020801624,1.481481481
1.02130898,1.432098765
1.021816337,1.839506173
1.022323694,2.839506173
1.02283105,2.790123457
1.023338407,2.543209877
1.023845764,3.037037037
1.02435312,3.938271605
1.024860477,3.814814815
""")

df = pd.read_csv(test_data)

slopes = theilslopes(df.y, df.x)

df['line'] = df.x * slopes[0] + slopes[1]
df['line_corr'] = df.x * slopes[0] + (df.y - slopes[0] * df.x).median()

df.plot(x='x', y=['y', 'line', 'line_corr'], label=['Data', 'Theilslope intercept', 'Corrected Intercept'])
plt.show()

Scipy/Numpy/Python version information:

import sys, scipy, numpy; print(scipy.__version__, numpy.__version__, sys.version_info)
# 1.7.0 1.21.0 1.2.5 sys.version_info(major=3, minor=9, micro=5, releaselevel='final', serial=0)

[chrisb83]

@atrevisan21 thanks for the additional research on this topic.

I think the best approach would be to add a new keyword method like in stats.siegelslopes:

method='...': compute intercept as median(y) - medslope*median(x)) (default option to keep backwards compatibility) method='...': compute intercept as median(y - medslope*x)

Not sure what a good name for the arguments would be, maybe ‘separate’ in the first case since the medians are computed separately and ‘joint’ in the second case?

[atrevisan21]

It seems like there are two ways to calculate the intercept both np.median(y) - np.median(x) * m and np.median(y - x * m) ( Helsel and others, 2019 pg. 268). The main benefit of finding the slopes using the median of x and the median of y is that the line will pass through point median x and median y mirroring least squares regression passing through mean x and mean y.

There doesn’t seem to be a ‘right’ way to calculate the intercept because the estimator is mostly focused around the slope according to this stack exchange discussion. The choice of intercept calculation seems more circumstantial than definitive.

It looks like the USGS program KTRLine uses the median(y) - median(x) * slope approach (Conover, 1980) and so does the R package. It may be better to leave the intercept as is to be consistent with other software programs. The user can change the calculation if needed. Maybe a note could be added to the docstring.