Discontinuities in scipy.special.mathieu_a

Hi, this is to report an issue with scipy.special.mathieu_a, which is likely related to the issue previously reported in #4479. While #4479 reported discontinuities when varying the order n at fixed q, this reports discontinuities when varying the value of q for fixed n.

The following code,

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import mathieu_a, mathieu_b

fig, ax = plt.subplots()
n = 4
qs = qs = np.linspace(600, 1500, 100)
ax.plot(qs, -2*qs+2*(2*n+1)*np.sqrt(qs)-((2*n+1)**2+1)/8, '-c', label = 'Analytical')
ax.plot(qs, mathieu_a(n, qs), '--r', label = 'SciPy')
plt.title('mathieu_a for n=4 over range of q\'s')
plt.legend()
plt.show()

results in the plot

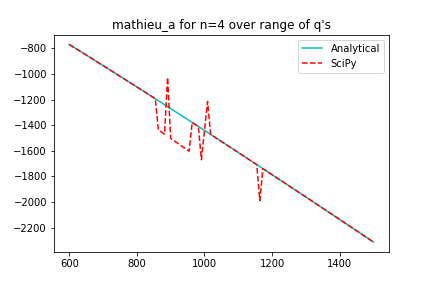
which possesses discontinuities that I think is not expected analytically. For reference, the “large q limit” analytical expression was obtained from DLMF.

(I’m using Python 3.7.7, numpy-1.21.1 and scipy-1.7.1)

[cw-tan]

@czgdp1807 Thank you for the fix, I really appreciate it! I’m not too familiar with how REFINE works and how necessary it is to have it, so I don’t think I’d be able to give a good assessment of which solution is better, but from the sound of it, it seems like with your second approach, the benefits of REFINE are maintained and the bumps caused by it are avoided, which sounds better than just not using REFINE, assuming that the error reduction due to REFINE is somewhat crucial for most applications.

However, one thing I’d comment on is that the “analytical expression” I used to compare the SciPy result against is just the first few terms of the “large q limit” expression from DLMF, so I’m not sure how reliable it is as a benchmark. I truncated the asymptotic expression at the first term that was a reciprocal in q, i.e. the term with 1/h or 1/sqrt(q) in DLMF expression (this term and following ones were not included). Just doing a quick calculation with my calculator for the 4th order mathieu_a with q = 1000, that term would be about 0.187 (3sf) if I’m not mistaken, which could be numerically significant if it is comparable to the magnitude of the changes you get when you imposed the fix.

In case you’re still using the “analytical expression” in my code as a benchmark, I think maybe including one or two more terms in the asymptotic expansion would be safer if you’re assessing the quality of the fix based on how much the numerical result deviates from the “analytical” values.

[czgdp1807]

After adding those terms, the bumps are still there in master branch. However, in my diff, those are removed. The secant method is a bit unstable (the one used by REFINE). Combining it with BISECTION_REFINE, removes the discontinuities wherever they are present and if REFINE works correctly for an input then it will keep doing so, since, bisection method just brings A closer to the root which is anyways good for secant method.