Faster implementation of scipy.sparse.block_diag

Before making a move on this, I would like to put this potential enhancement out on GitHub to discuss, to gauge interest first. I’m hoping this discussion reveals something fruitful, perhaps even something new that I can learn, and it doesn’t necessarily have to result in a PR.

For one of my projects involving message passing neural networks, which operate on graphs, I use block diagonal sparse matrices a lot. I found that the bottleneck is in the block_diag creation step.

To verify this, I created a minimal reproducible example, using NetworkX.

Reproducing code example:

import networkx as nx
import numpy as np
from scipy.sparse import block_diag, coo_matrix
import matplotlib.pyplot as plt

Gs = []
As = []
for i in range(50000):
    n = np.random.randint(10, 30)
    p = 0.2
    G = nx.erdos_renyi_graph(n=n, p=p)
    Gs.append(G)
    A = nx.to_numpy_array(G)
    As.append(A)

In a later Jupyter notebook cell, I ran the following code block.

%%time
block_diag(As)

If we vary the number of graphs that we create a block diagonal matrix on, we can time the block_diag function, which I did, resulting in the following chart:

Some additional detail:

• 3.5 seconds for 5,000 graphs, 97,040 nodes in total.
• 13.3 seconds for 10,000 graphs, 195,367 nodes in total. (2x the inputs, ~4x the time)
• 28.2 seconds for 15,000 graphs, 291,168 nodes in total. (3x the inputs, ~8x the time)
• 52.9 seconds for 20,000 graphs, 390,313 nodes in total. (4x the inputs, ~16x the time)

My expectation was that block_diag should scale linearly with the number of graphs. However, the timings clearly don’t show that.

I looked into the implementation of block_diag in scipy.sparse, and found that it makes a call to bmat, which considers multiple cases for array creation. That said, I wasn’t quite clear how to make an improvement to bmat, thus, I embarked on an implementation that I thought might be faster. The code looks like such:

def block_diag_nojit(As: List[np.array]):
    row = []
    col = []
    data = []
    start_idx = 0
    for A in As:
        nrows, ncols = A.shape
        for r in range(nrows):
            for c in range(ncols):
                if A[r, c] != 0:
                    row.append(r + start_idx)
                    col.append(c + start_idx)
                    data.append(A[r, c])
        start_idx = start_idx + nrows
    return row, col, data
                    
row, col, data = block_diag_nojit(As)

Profiling the time for this:

CPU times: user 7.44 s, sys: 146 ms, total: 7.59 s
Wall time: 7.58 s

And just to be careful, I ensured that the resulting row, col and data were correct:

row, col, data = block_diag_nojit(As[0:10])
amat = block_diag(As[0:10])

assert np.allclose(row, amat.row)
assert np.allclose(col, amat.col)
assert np.allclose(data, amat.data)

I then tried JIT-ing the function using numba:

%%time
row, col, data = jit(block_diag_nojit)(As)

Profiling the time:

CPU times: user 1.27 s, sys: 147 ms, total: 1.42 s
Wall time: 1.42 s

Creating the coo_matrix induces a flat overhead of about 900ms, thus it is most efficient to call coo_matrix outside of the block_diag_nojit function:

# This performs at ~2 seconds with the scale of the graphs above.
def block_diag(As):
    row, col, data = jit(block_diag_nojit)(As)
    return coo_matrix((data, (row, col)))

For a full characterization:

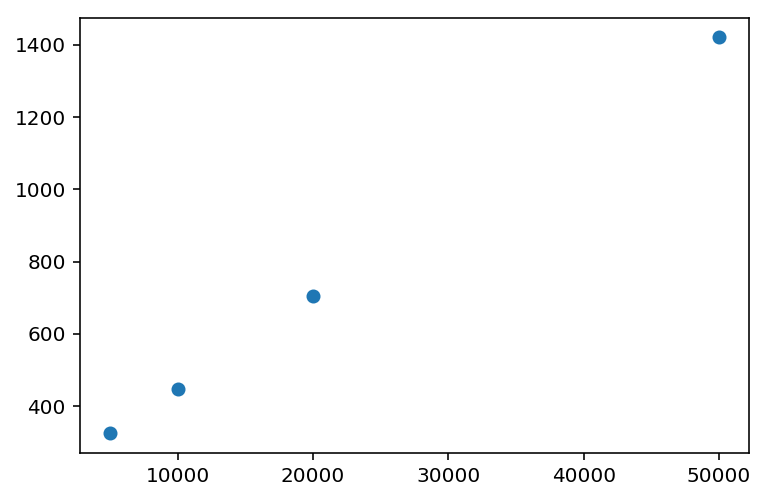
(This is linear in the number of graphs.)

I’m not quite sure why the bmat-based block_diag implementation is super-linear, but my characterization of this re-implementation shows that it is up to ~230x faster with JIT-ing, and ~60x faster without JIT-ing (at the current scale of data). More importantly, the time taken is linear with the number of graphs, and not raised to some power.

I am quite sure that the block_diag matrix implementation, as it currently stands, was built with a goal in mind that I’m not aware of, which necessitated the current implementation design (using bmat). That said, I’m wondering if there might be interest in a PR contribution with the aforementioned faster block_diag function? I am open to the possibility that this might not be the right place, in which I’m happy to find a different outlet.

Thank you for taking the time to read this!

[ludcila]

Hi, I am also interested in contributing to the scipy repository, and thought this was a good place to get started, thanks to the guidance from @ericmjl and @perimosocordiae. I hope it is ok if I try to tackle this issue as well. So far, I believe I have been able to reproduce @ericmjl’s findings. This is what I have:

• I rewrote sparse.block_diag as proposed by @ericmjl with some minor changes
• Unit tests are passing
• Added a benchmark test that shows the improvement in performance (from O(N^2) to O(N))

def block_diag(mats, format='coo', dtype=None):
    dtype = np.dtype(dtype)
    row = []
    col = []
    data = []
    r_idx = 0
    c_idx = 0
    for ia, a in enumerate(mats):
        if issparse(a):
            a = a.tocsr()
        else:
            a = coo_matrix(a).tocsr()
        nrows, ncols = a.shape
        for r in range(nrows):
            for c in range(ncols):
                if a[r, c] is not None:
                    row.append(r + r_idx)
                    col.append(c + c_idx)
                    data.append(a[r, c])
        r_idx = r_idx + nrows
        c_idx = c_idx + ncols
    return coo_matrix((data, (row, col)), dtype=dtype).asformat(format)

class Construct(Benchmark):
    param_names = ['num_matrices']
    params = [ 1000, 5000, 10000, 15000, 20000 ]
    
    def setup(self, num_matrices):
        self.matrices = []
        for i in range(num_matrices):
            rows = np.random.randint(1,  4)
            columns = np.random.randint(1, 4)
            mat = np.random.randint(0, 10, (rows, columns))
            self.matrices.append(mat)
            
    def time_block_diag(self, num_matrices):
        sparse.block_diag(self.matrices)

Original implementation: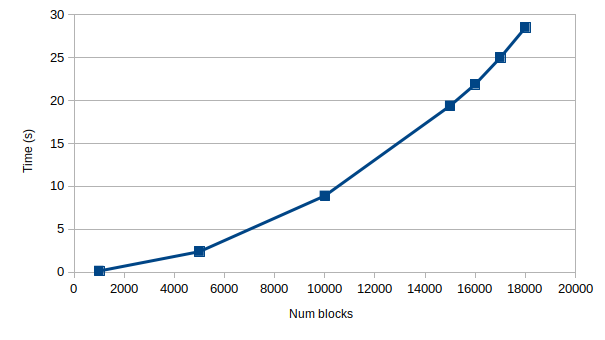 (the benchmark fails due to time out for 19 and 20 k)

Proposed implementation: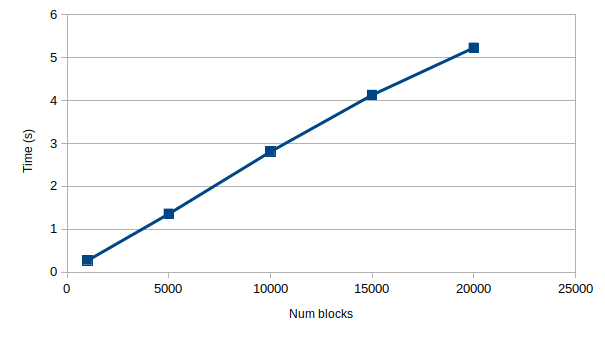

There are only three tests for this particular method, and I am not confident that I did not break anything 😃 could you please have a look at what I did and let me know if it is OK enough for a PR, or if there is anything else I should do as a next step? Thank you so much!

[ericmjl]

@ludcila wonderful work! FWIW, I also learned a thing here - didn’t realize there was a benchmarking framework!