Incorrect generalization for binomial/nCr

https://github.com/scipy/scipy/blob/701ffcc8a6f04509d115aac5e5681c538b5265a2/scipy/special/orthogonal_eval.pxd#L72-L76

nCr is only undefined if n<0, n is an integer, AND k is not an integer. nCr is perfectly defined for negative n and integer k. line 74 should be

if n == nx and k != floor(k):

[steppi]

To an extent I agree, when binomial coefficients \binom{n}{k}, are considered as functions of two integer variables, then they are usually defined for negative integers n. But strictly speaking, when \binom{x}{y} is treated as a function of two real variables, I don’t think it’s unreasonable to say it is undefined for x a negative integer and y an integer.

For the case of two real variables,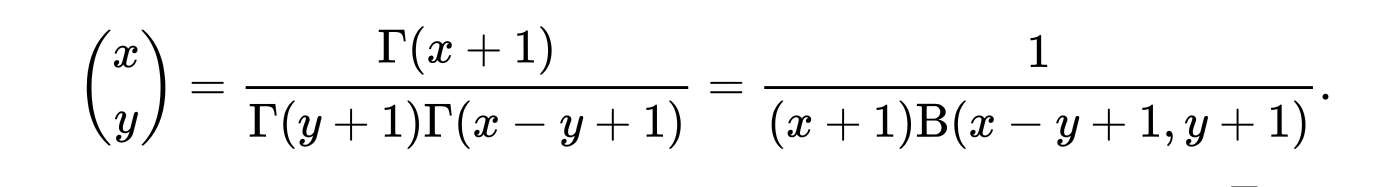 \binom{x}{y} is typically defined by

where Γ is the Gamma function and Β is the Beta function.

The value of the limit as (x, y) tends to (-n, k) for -n a negative integer and k an integer depends on the direction in which (x, y) approaches (-n, k). Since the binomial coefficient is not continuous at these points, I think the authors of the function made a reasonable choice to treat it as undefined there. Also, at this time, there’s likely to be downstream code that depends upon this choice, so it may break some user code to change things now.

Your issue does raise a very nice point thought. This function was originally implemented as an internal function for orthogonal polynomial evaluation and only later exposed in the public API. It doesn’t have a proper docstring at this time and I think it could really use one that explains the choices made.

[HexCodeFFF]

Sure!