WIP: Addition of MLE for stats.invgauss/wald

Part of the #11782 issue.

@mdhaber,

I have been investigating the maximum likelihood estimators given in Chapter 25, Inverse Gaussian (Wald) Distribution, but the results from the MLEs don’t seem to come close to the results of either the wald or invgauss distributions in scipy.

Here is how the PDF is described in the textbook we have been using, on page 120:

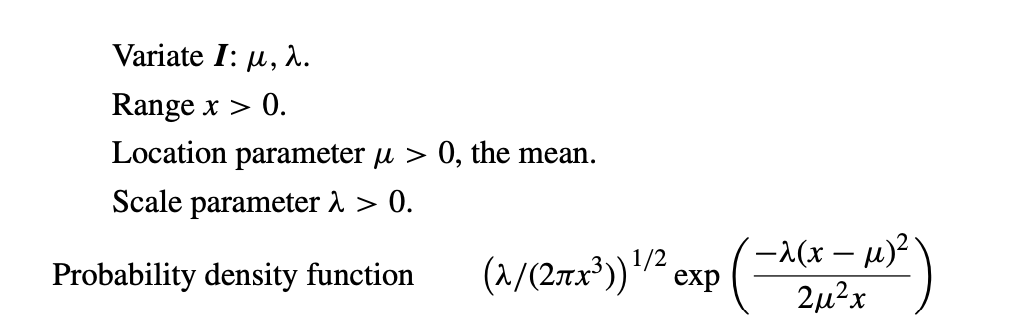
And here are the equations for MLE.

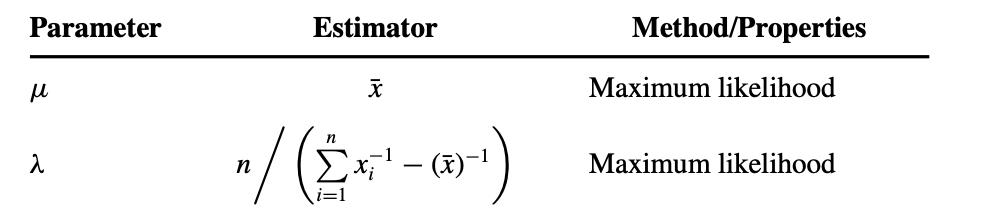
It may be another issue with terminology, since the use of mu to represent the location, as the textbook describes, is implemented as a shape parameter in stats.invgauss. However, the mean of a random generate only appears to represent the mu used in generation when loc and scale are the standard loc=0, scale=1.

For example,

from scipy.stats import invgauss
data = invgauss.rvs(mu=3.25, size=10000)
print(data.mean())

=> 3.223328.... Just one example, but it appears that in general it matches.

With other location and scale values it doesn’t match.

from scipy.stats import invgauss
data = invgauss.rvs(mu=3.25, scale=2, size=10000)
print(data.mean())

=> 6.62447.... Just one example, but in general they don’t match.

The code for the scale is

scale = len(data) / (np.sum(data**(-1) - mu**(-1)))

and I played around with both of these equations quite a bit to try to get them to match up with / or be better than the default fit method, but other than the relation I described above, I’m not sure that these will work for these distributions. It may be possible to use the mean to determine the shape parameter in invgauss if the person has already fixed floc=0, scale=1, but that seems like a very niche usage.

What are your thoughts?

[mdhaber]

I think if you go a bit further, you’ll find with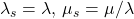 loc=0 that they are equivalent with

So if the user passes in floc=0, you could use the equations from the book to get the book’s version of the parameters, then use the relationships above to get SciPy’s parameters.

Update: Yes:

import numpy as np
from scipy.stats import invgauss
data = invgauss.rvs(mu=3.25, scale=2, size=1000000)

mu = np.mean(data)
s = len(data) / (np.sum(data**(-1) - mu**(-1)))
mu_s = mu/s
print(mu_s, s)

gives

3.2698217368812785 1.9933346841496646

If the user doesn’t pass in floc=0, then you could at least use the analytical solution above (assuming floc=0) as a guess to the super fit method. You might try following @WarrenWeckesser’s argument here about weibull_min to see if it applies to this distribution.

[swallan]

@mdhaber @WarrenWeckesser

Thanks for the pointers! I really appreciate it. I’ll create a PR for this soon.