Reflected light
See original GitHub issueI figured out the general expressions for the total flux visible from each polynomial term in the case that the disk is bounded by an elliptical terminator segment of semi-minor axis b. Assuming this is our geometry,
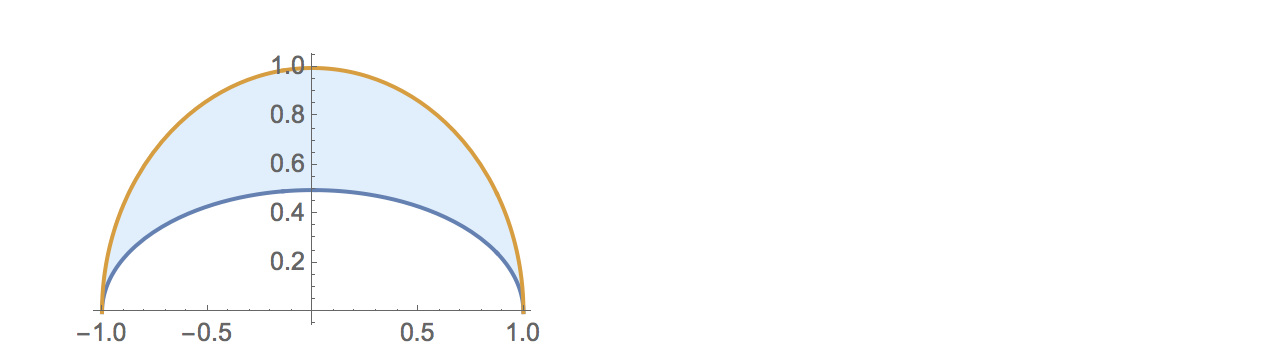
the expressions for the case where the planet is between new phase and half phase are
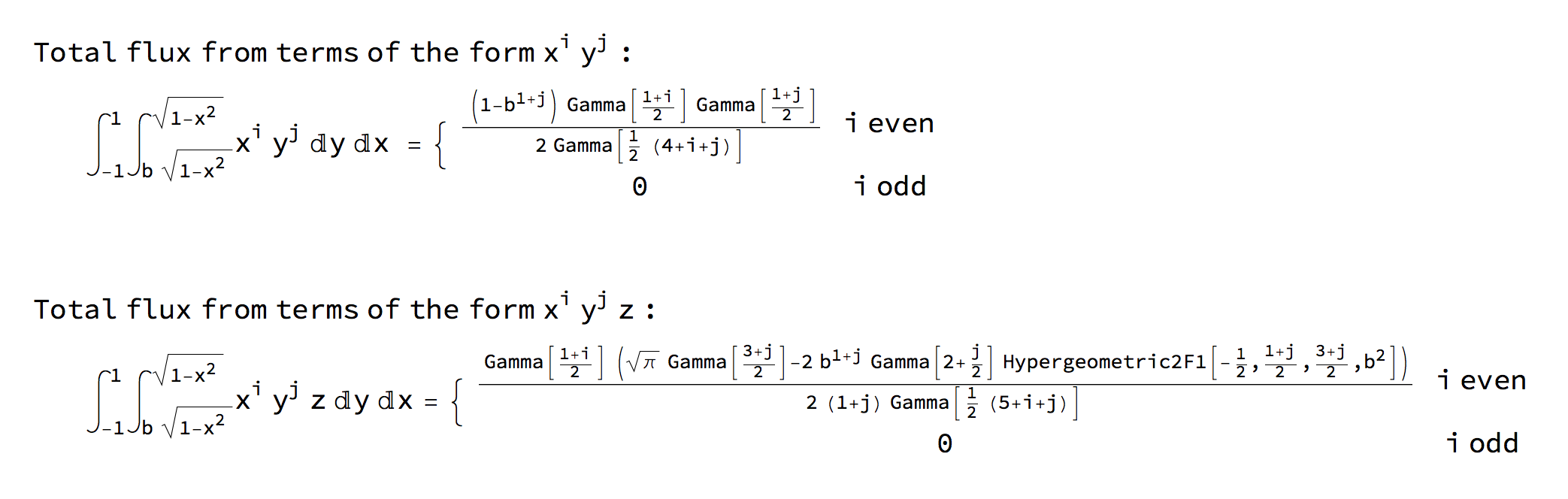
Issue Analytics
- State:
- Created 5 years ago
- Reactions:1
- Comments:5 (2 by maintainers)
 Top Results From Across the Web
Top Results From Across the Web
Introduction to Reflected Light Microscopy | Olympus LS
Reflected light microscopy is often referred to as incident light, epi-illumination, or metallurgical microscopy, and is the method of choice for ...
Read more >What is Reflection of Light? - Definition, Laws, Types & Video
When a ray of light approaches a smooth polished surface and the light ray bounces back, it is called the reflection of light....
Read more >definition of reflected light by The Free Dictionary
The sensation of perceiving light; brightness: a sudden light that made me blink. 3. a. A source of light, especially a lamp, a...
Read more >Reflection and refraction - light - Britannica
Light rays change direction when they reflect off a surface, move from one transparent medium into another, or travel through a medium whose...
Read more >What is reflected light in photography – essential for portraits ...
Reflected light takes on the color cast of the surface used to reflect it. So, when you bounce light off of a green...
Read more > Top Related Medium Post
Top Related Medium Post
No results found
 Top Related StackOverflow Question
Top Related StackOverflow Question
No results found
 Troubleshoot Live Code
Troubleshoot Live Code
Lightrun enables developers to add logs, metrics and snapshots to live code - no restarts or redeploys required.
Start Free Top Related Reddit Thread
Top Related Reddit Thread
No results found
 Top Related Hackernoon Post
Top Related Hackernoon Post
No results found
 Top Related Tweet
Top Related Tweet
No results found
 Top Related Dev.to Post
Top Related Dev.to Post
No results found
 Top Related Hashnode Post
Top Related Hashnode Post
No results found

And, as you foresaw, the first two terms are straightforward:
I_0 = \tfrac{1}{2} \left(-b\sqrt{1-b^2}+\cos^{-1} b\right)and
I_1 = \tfrac{1}{3} (1-b^2)^{3/2}.@rodluger Let:
I_j(b) = \int_b^1 \alpha^j (1-\alpha^2)^{1/2} d\alphaThen, I find:
I_j = \frac{1}{j+2} \left[ b^{j-1}(1-b^2)^{3/2} + (j-1) I_{j-2}\right]which is your recursion relation! The first integral integrates to the Gamma function term which you gave above.